Introduction to C++11 Threads
Introduction
I decided to do this simple project in order to get used with the new thread class in C++11. The idea is to take two matrices and multiply them using different threads. I want to see how the implementation differs, the problems that may arise and how the execution time scales with the number of threads and the size of the matrices.
Matrix structure
First of all, let’s introduce the main structure used in this program, the Matrix:
struct Matrix {
float ** elements;
void initialize_random();
};
It’s as easy as that. One thing to note here is that I am using a two dimension array of pointers instead of just floats. This has a reason and it has to do with threads.
All threads in a program share the heap space BUT have their own memory space reserved for the stack. However, the stack size it’s quite small and can’t be modified in C++11. Since we are working with quite big matrices (1000x1000), it is better to just use the heap instead of the stack. For this reason, we use two dimensional array of pointers. Because it’s size can’t be known at compile tim,e it will be initialized in the heap, not in the stack.
Single thread solution
This code should be really straightforward, its just a standard matrix multiplication, nothing to explain:
void multiply(Matrix& r, const Matrix& m1, const Matrix& m2) {
for (int i = 0; i < MATRIX_SIZE; ++i) {
for (int j = 0; j < MATRIX_SIZE; ++j) {
float result = 0.0f;
for (int k = 0; k < MATRIX_SIZE; ++k) {
const float e1 = m1.elements[i][k];
const float e2 = m2.elements[k][j];
result += e1 * e2;
}
r.elements[i][j] = result;
}
}
}
Multi thread solution
The initialization of threads it’s also quite easy:
// Create an array of threads
std::thread threads[THREADS_NUMBER];
for (int i = 0; i < THREADS_NUMBER; ++i) {
// Initialize each thread with the function responsible of multiplying only a part of the matrices
threads[i] = std::thread(multiply_threading, r, i, m1, m2);
}
for (int i = 0; i < THREADS_NUMBER; ++i) {
// Wait until each thead has finished
threads[i].join();
}
The first thing that we do is we create an array of threads where we’ll store our threads. Then, we initialize each thread giving it the function to execute multiply_threading that has the following signature:
void multiply_threading(Matrix& result, const int thread_number, const Matrix& m1, const Matrix& m2);
The first parameter is the output matrix, The second parameter is the thread number (later on this) The third and the forth parameter are the matrices to be multiplied.
When initializing a thread with a function like before, all paremeters, by default, are passed by value, even that I have specified that I want them by reference. This is done automatically to prevent threads of writing the same memory address. This is ok most of the times but I don’t want my program to spend time copying huge matrices, I really want to pass by reference. To do so, we need to call std::ref(parameter) like this:
threads[i] = std::thread(multiply_threading, std::ref(r), i, std::ref(m1), std::ref(m2));
Now, all paremeters are passed by reference. We are saving a huge amount of time avoiding the copy of the matrices. Nevertheless, since now, all threads share the same data, we now have to make sure that they don’t write on the same memory addresses. To do it, I’ve implemented a clever algorithm such that each thread works only on a specific part of the matrix. This way we are sure that one and only one thread modifies each value. This is implemented in the previous declared function multiply_threading.
Before getting into the code, I am going to explain in with drawings because it is how I see it:
As you can see, this matrix can be easily translated into a one-dimensional array. The data is the same, the only thing that it changes it’s how we represent the internal structure to store it. This idea was useful for me to see how to split the work in the different threads, like this:
// Nº of elements of the matrix (= size of the one-dimensional array)
const int n_elements = (MATRIX_SIZE * MATRIX_SIZE);
// Nº of operations that each specific thread has to do
const int n_operations = n_elements / THREADS_NUMBER;
// Nº of operations that are left and someone has to do
const int rest_operations = n_elements % THREADS_NUMBER;
Quite easy huh? We’re just calculating the load of each thread. This load is given by the total number of operations divided by the number of workers (threads) that we had. Because this division may have a remainder, we have to take it into account.
So far, so good. We know the amount of work that each thread has to do and also the “extra work” (rest_operations). Now, we need to know in which part of the matrix this work should be done, avoiding overlapping (because of what we said earlier). This is where we are going to use the thread_number. The idea is very simple. The first thread is going to do its amount of work starting at the beginning of the matrix. The second thead is going to do its work starting at the end of the work of the first thread and so on. In code looks even easier:
int start_op = n_operations * thread_number; // Inclusive
int end_op = (n_operations * (thread_number + 1)); // Exclusive
Instead of working directly in the matrix, we calculate the indices in the one-dimensional array because its easier. Suppose that we have a 3x3 matrix and 3 threads:
- Thread 0:
- start_op = 3 * 0 = 0
- end_op = 3 * (0 + 1) = 3;
- Thread 1:
- start_op = 3 * 1 = 0
- end_op = 3 * (1 + 1) = 3;
- Thread 2:
- start_op = 3 * 2 = 6
- end_op = 3 * (2 + 1) = 9;
See? The first thread does the first three multiplications, the second three more…But what happens to we do with the remainder of operations? Well, in reality the code doesn’t look like before. We have to add an if statemente to detect this edge case:
int start_op, end_op;
if (thread_number == 0) {
// First thread does more job
start_op = n_operations * thread_number;
end_op = (n_operations * (thread_number + 1)) + rest_operations;
}
else {
start_op = n_operations * thread_number + rest_operations;
end_op = (n_operations * (thread_number + 1)) + rest_operations;
}
I’ve decided to put the remainder of the jobs to the first thread. Since it’s the one that it’s created first, this should be the more sensible way of doing it. I’ve just added the rest operations to the end index. Then, I add the rest operations as an offset to the start and end indices to all the other threads. Now, assume that our matrix is 4x4 but we have 3 threads:
- Thread 0:
- start_op = 5 * 0 = 0
- end_op = 5 * (0 + 1) + 1 = 6;
- Thread 1:
- start_op = 5 * 1 + 1 = 6
- end_op = 5 * (1 + 1) + 1 = 11;
- Thread 2:
- start_op = 5 * 2 + 1 = 11
- end_op = 5 * (2 + 1) + 1 = 16;
Cool, we know what each thread has to do, so let’s do the actual multiplication:
for (int op = start_op; op < end_op; ++op) {
// Translate one-d index to two-d index
const int row = op % MATRIX_SIZE;
const int col = op / MATRIX_SIZE;
float r = 0.0f;
for (int i = 0; i < MATRIX_SIZE; ++i) {
const float e1 = m1.elements[row][i];
const float e2 = m2.elements[i][col];
r += e1 * e2;
}
result.elements[row][col] = r;
}
It’s very simple. We go from the start to the end of operations and we convert from 1-d array to 2-d and then we just perform the row * col matrix multiplication.
The complete function code is displayed below:
void multiply_threading(Matrix& result, const int thread_number, const Matrix& m1, const Matrix& m2) {
// Calculate workload
const int n_elements = (MATRIX_SIZE * MATRIX_SIZE);
const int n_operations = n_elements / THREADS_NUMBER;
const int rest_operations = n_elements % THREADS_NUMBER;
int start_op, end_op;
if (thread_number == 0) {
// First thread does more job
start_op = n_operations * thread_number;
end_op = (n_operations * (thread_number + 1)) + rest_operations;
}
else {
start_op = n_operations * thread_number + rest_operations;
end_op = (n_operations * (thread_number + 1)) + rest_operations;
}
for (int op = start_op; op < end_op; ++op) {
const int row = op % MATRIX_SIZE;
const int col = op / MATRIX_SIZE;
float r = 0.0f;
for (int i = 0; i < MATRIX_SIZE; ++i) {
const float e1 = m1.elements[row][i];
const float e2 = m2.elements[i][col];
r += e1 * e2;
}
result.elements[row][col] = r;
}
}
Benchmarking
To measure the execution time of the two different methods I executed 1.000 multiplications of each method. Then I just calculated the average execution time:
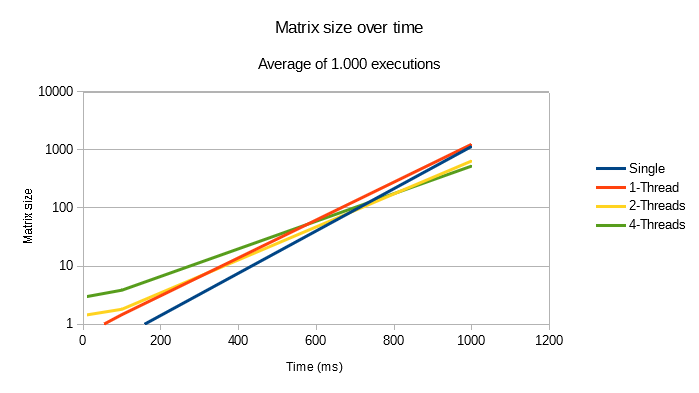
At the beginning of the chart, the single execution in the main thread of more efficient because the workload is very small. The multi-thread execution is very slow because, even that they work in parallel, the workload is so small that it doesn’t compensate for the overhead of creating, initializing and joining the threads.
Nevertheless, as the workload increases (the matrices get bigger) the multi-threading options gets better and better. This is, obviusly, because each time, more and more work can be performed in parallel and the overhead is very small in comparision to the calculation time.
References
C++ Multithreading, https://www.tutorialcup.com/cplusplus/multithreading.htm
MULTI-THREADED PROGRAMMING TERMINOLOGY in C++- 2017, http://www.bogotobogo.com/cplusplus/multithreaded.php