Definition

Even though in graphics we use 3D triangles, the surface of a triangle always lies in a 2D plane. It makes sense then, to have a specific coordinate space to work with the surface independently of the 3D space. This coordinate system is called barycentric space and is a local coordinate system for triangles (in fact, for simplexes) that allows us to express any point on the surface as a weighted average of the vertices. These weights are known as barycentric coordinates:

Here, p(x,y,z) is just a 3D point in the space that lies in the same plane that the triangle and can be expressed as a linear combination of the vertices of the triangle V1, V2, V3 and the barycentric coordinates u, v, w. If you think about it, Cartesian coordinates can also be expressed as a linear combination of its basis vectors. However, the difference remains that the sum of the barycentric coordinates should be one:

This constraint removes one degree of freedom and is the reason why, even that we have three cordinates, the result is in a 2D space. This may seem a little bit difficult to understand, so let’s do it more visual and we’ll come back with that later.

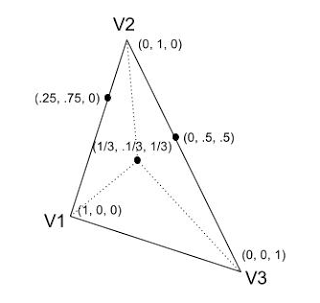
First of all, we can see that at the vertices of the triangles, one barycentric coordinate is exactly one while the others are zero:

Secondly, we see that, at the edges, the barycentric coordinate corresponding to the opposite vertex is exactly zero. In addition, points that are inside of the triangle (between edges) have positive values for barycentric coordinates while the points outside the triangle have negative values. Barycentric space tessellates the space intro triangles of the same size:

Another way to think about barycentric coordinates is to make up a 2D coordinate system in which one vertex of the triangle is the origin, and the other two vertices minus the origin make the basis vectors:

The coordinate system would look like this:

Now it is very clear that we only have two degrees of freedom and therefore, all points of the barycentric space lie on the same 2D plane.

Use case

Barycentric coordinates are very useful in 2D and 3D graphics. Most graphic applications use them because they provide an easy way to interpolate the value of attributes (color, textures, normals…) between vertices. This can be done because, by definition, barycentric coordinates express “how much of each vertex does a point have”.

For a programmer, it would be exhausting (and impossible) to specify the value of each of these attributes at each point in the surface. So, what we do is, we specify the value of the attributes at the vertices and then we use barycentric coordinates to interpolate the rest of the points.

In the following triangle, I’ve set the vertices to green, blue and red and then I’ve interpolated the color of the rest of the points using barycentric coordinates:

In the rasterizer that I am implementing right now (the previous image was generated with it) I use barycentric coordinates to interpolate colors, texture coordinates and normals and depth. The latter is probably the most common use of barycentric coordinates. Is the (only?) way to compute the depth of a pixel in screen space to do the depth-buffering and check which object is closer.

Another frequent use is to use the barycentric coordinates to check if a point is inside, on the edge, or outside the triangle. As we saw:

• If all barycentric coordinates of a point are positive and sum one, they point lies inside the triangle.
• If one barycentric coordinate is zero and the other ones are positive and less than one, the point lies on an edge.
• If any barycentric coordinate is negative, the point is outside the triangle.

References

Fletcher Dunn, Ian Parberry: “3D Math Primer for Graphics and Game Development”